Ti

Dijkstra算法用于路由协议挺不错的，转来参考下

Dijkstra算法是典型最短路算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解，但由于它遍历计算的节点很多，所以效率低。
Dijkstra算法是很有代表性的最短路算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。
Dijkstra一般的表述通常有两种方式，一种用永久和临时标号方式，一种是用OPEN, CLOSE表方式，Drew为了和下面要介绍的 A* 算法和 D* 算法表述一致，这里均采用OPEN,CLOSE表的方式。

Dijkstra算法-大概过程
创建两个表，OPEN, CLOSE。

OPEN表保存所有已生成而未考察的节点，CLOSED表中记录已访问过的节点。
1． 访问路网中里起始点最近且没有被检查过的点，把这个点放入OPEN组中等待检查。
2． 从OPEN表中找出距起始点最近的点，找出这个点的所有子节点，把这个点放到CLOSE表中。
3． 遍历考察这个点的子节点。求出这些子节点距起始点的距离值，放子节点到OPEN表中。
4． 重复2，3，步。直到OPEN表为空，或找到目标点。

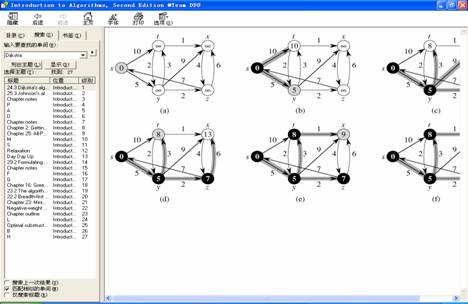
样例图:

输入格式:

输出格式:

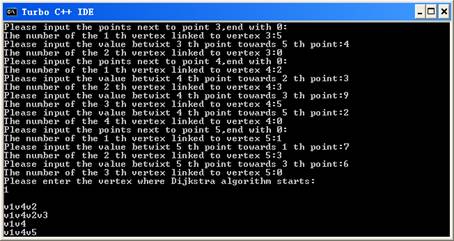
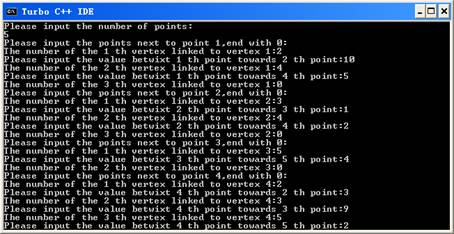
输入时，将s,t,x,y,z五个点按照1,2,3,4,5起别名，输入格式按照下图例所示

当提示Please enter the vertex where Dijkstra algorithm starts:时输入算法的起始点

比如计算结果v1v4v2表示从点1到点2经过1，4，2为最短路径

Dijkstra算法的完整实现版本，算法的源代码

/* Dijkstra.c

Copyright (c) 2002, 2006 by tiham.com

All Rights Reserved.

*/

#include “stdio.h”

#include “malloc.h”

#define maxium 32767

#define maxver 9 /*defines the max number of vertexs which the programm can handle*/

#define OK 1

struct Point

{

char vertex[3];

struct Link *work;

struct Point *next;

};

struct Link

{

char vertex[3];

int value;

struct Link *next;

};

struct Table /*the workbannch of the algorithm*/

{

int cost;

int Known;

char vertex[3];

char path[3];

struct Table *next;

};

int Dijkstra(struct Point *,struct Table *);

int PrintTable(int,struct Table *);

int PrintPath(int,struct Table *,struct Table *);

struct Table * CreateTable(int,int);

struct Point * FindSmallest(struct Table *,struct Point *);/*Find the vertex which has the smallest value reside in the table*/

int main()

{

int i,j,num,temp,val;

char c;

struct Point *poinpre,*poinhead,*poin;

struct Link *linpre,*linhead,*lin;

struct Table *tabhead;

poinpre=poinhead=poin=(struct Point *)malloc(sizeof(struct Point));

poin->next=NULL;

poin->work=NULL;

restart:

printf(“Notice:if you wanna to input a vertex,you must use the format of number!\n”);

printf(“Please input the number of points:\n”);

scanf(“%d”,&num);

if(num>maxver||num<1||num%1!=0)

{

printf(“\nNumber of points exception!”);

goto restart;

}

for(i=0;i<num;i++)

{

printf(“Please input the points next to point %d,end with 0:\n”,i+1);

poin=(struct Point *)malloc(sizeof(struct Point));

poinpre->next=poin;

poin->vertex[0]=’v’;

poin->vertex[1]=’0’+i+1;

poin->vertex[2]=’\0′;

poin->work=(struct Link *)malloc(sizeof(struct Link));

linpre=lin=poin->work;

linpre->next=NULL;

for(j=0;j<num-1;j++)

{

printf(“The number of the %d th vertex linked to vertex %d:”,j+1,i+1);

scanf(“%d”,&temp);

if(temp==0)

{

lin->next=NULL;

break;

}

else

{

lin=(struct Link *)malloc(sizeof(struct Link));

linpre->next=lin;

lin->vertex[0]=’v’;

lin->vertex[1]=’0’+temp;

lin->vertex[2]=’\0′;

printf(“Please input the value betwixt %d th point towards %d th point:”,i+1,temp);

scanf(“%d”,&val);

lin->value=val;

linpre=linpre->next;

lin->next=NULL;

}

}

poinpre=poinpre->next;

poin->next=NULL;

}

printf(“Please enter the vertex where Dijkstra algorithm starts:\n”);

scanf(“%d”,&temp);

tabhead=CreateTable(temp,num);

Dijkstra(poinhead,tabhead);

PrintTable(temp,tabhead);

return OK;

}

struct Table * CreateTable(int vertex,int total)

{

struct Table *head,*pre,*p;

int i;

head=pre=p=(struct Table *)malloc(sizeof(struct Table));

p->next=NULL;

for(i=0;i<total;i++)

{

p=(struct Table *)malloc(sizeof(struct Table));

pre->next=p;

if(i+1==vertex)

{

p->vertex[0]=’v’;

p->vertex[1]=’0’+i+1;

p->vertex[2]=’\0′;

p->cost=0;

p->Known=0;

}

else

{

p->vertex[0]=’v’;

p->vertex[1]=’0’+i+1;

p->vertex[2]=’\0′;

p->cost=maxium;

p->Known=0;

}

p->next=NULL;

pre=pre->next;

}

return head;

}

int Dijkstra(struct Point *p1,struct Table *p2) /* Core of the programm*/

{

int costs;

char temp;

struct Point *poinhead=p1,*now;

struct Link *linna;

struct Table *tabhead=p2,*searc,*result;

while(1)

{

now=FindSmallest(tabhead,poinhead);

if(now==NULL)

break;

result=p2;

result=result->next;

while(result!=NULL)

{

if(result->vertex[1]==now->vertex[1])

break;

else

result=result->next;

}

linna=now->work->next;

while(linna!=NULL) /* update all the vertexs linked to the signed vertex*/

{

temp=linna->vertex[1];

searc=tabhead->next;

while(searc!=NULL)

{

if(searc->vertex[1]==temp)/*find the vertex linked to the signed vertex in the table and update*/

{

if((result->cost+linna->value)<searc->cost)

{

searc->cost=result->cost+linna->value;/*set the new value*/

searc->path[0]=’v’;

searc->path[1]=now->vertex[1];

searc->path[2]=’\0′;

}

break;

}

else

searc=searc->next;

}

linna=linna->next;

}

}

return 1;

}

struct Point * FindSmallest(struct Table *head,struct Point *poinhead)

{

struct Point *result;

struct Table *temp;

int min=maxium,status=0;

head=head->next;

poinhead=poinhead->next;

while(head!=NULL)

{

if(!head->Known&&head->cost<min)

{

min=head->cost;

result=poinhead;

temp=head;

status=1;

}

head=head->next;

poinhead=poinhead->next;

}

if(status)

{

temp->Known=1;

return result;

}

else

return NULL;

}

int PrintTable(int start,struct Table *head)

{

struct Table *begin=head;

head=head->next;

while(head!=NULL)

{

if((head->vertex[1]-‘0’)!=start)

PrintPath(start,head,begin);

head=head->next;

}

return OK;

}

int PrintPath(int start,struct Table *head,struct Table *begin)

{

struct Table *temp=begin->next,*p,*t;

p=head;

t=begin;

if((p->vertex[1]-‘0’)!=start&&p!=NULL)

{

while(temp->vertex[1]!=p->path[1]&&temp!=NULL)

temp=temp->next;

PrintPath(start,temp,t);

printf(“%s”,p->vertex);

}

else

if(p!=NULL)

printf(“\n%s”,p->vertex);

return OK;

}